Introduction
The Bradley-Terry model is a simple model to rank different individuals. This is done by assuming that
\(P(i\text{ beats } j)=\frac{p_i}{p_i+p_j}.\)
Where \(p_k\) is some fitness value for the players. This simple model can be extended to include ties, home side advantages etc, but for now we will limit ourselves to the simple case.
A feature of this model is that if \(i\) is twice as likely to beat \(j\) than \(j\) is to beat \(i\) we will have that \(p_i=2p_j\). However, if absolute differences are desired one can use \(p_k=e^{S\beta_k}\) such that \(\beta_i=\beta_j+\gamma\) for some \(\gamma\) when \(i\) is twice as likely to beat \(j\). In fact the Elo-rating system uses \(S=\frac{\log(10)}{400}\). Since scaling can be done afterwards we will use \(p_k=e^{\beta_k}\).
We will now derive the maximum likelihood estimate and the associated confidence intervals.
Likelihood
Let us take \(w_{ij}\) to be the amount of times that \(i\) has beaten \(j\). Then the likelihood of \(i\) beating \(j\) \(w_{ij}\) times and \(j\) beating \(i\) \(w_{ji}\) times is given by
\[\binom{w_{ij}+w_{ji}}{w_{ij}}\left(\frac{e^{\beta_i}}{e^{\beta_i}+e^{\beta_j}}\right)^{w_{ij}}\left(\frac{e^{\beta_j}}{e^{\beta_i}+e^{\beta_j}}\right)^{w_{ji}}\]
We can use this to determine the squared likelihood function for all results (it is squared since all results are considered exactly twice).
\[L(\boldsymbol{\beta})^2=\prod^n_{i}\prod^n_{j}\binom{w_{ij}+w_{ji}}{w_{ij}}\left(\frac{e^{\beta_i}}{e^{\beta_i}+e^{\beta_j}}\right)^{w_{ij}}\left(\frac{e^{\beta_j}}{e^{\beta_i}+e^{\beta_j}}\right)^{w_{ji}}\]
This will result in the following log-likelihood
\[\begin{aligned}
2l(\boldsymbol{\beta}) &= \sum^n_{i}\sum^n_{j}\left[\log\left(\binom{w_{ij}+w_{ji}}{w_{ij}}\right)+w_{ij}\log\left(\frac{e^{\beta_i}}{e^{\beta_i}+e^{\beta_j}}\right)+w_{ji}\log\left(\frac{e^{\beta_j}}{e^{\beta_i}+e^{\beta_j}}\right)\right]\\
&\sim \sum^n_{i}\sum^n_{j}\left[w_{ij}\log\left(\frac{e^{\beta_i}}{e^{\beta_i}+e^{\beta_j}}\right)+w_{ji}\log\left(\frac{e^{\beta_j}}{e^{\beta_i}+e^{\beta_j}}\right)\right]\\
&=2\sum^n_{i}\sum^n_{j}\left[w_{ij}\log\left(\frac{e^{\beta_i}}{e^{\beta_i}+e^{\beta_j}}\right)\right].\end{aligned}\]
So, the log-likelihood is given by,
\[l(\boldsymbol{\beta})= \sum^n_{i}\sum^n_{j}w_{ij}\log\left(\frac{e^{\beta_i}}{e^{\beta_i}+e^{\beta_j}}\right)=\sum^n_{i}\sum^n_{j}w_{ij}\left(\beta_i-\log\left(e^{\beta_i}+e^{\beta_j}\right)\right).\]
We get the maximum likelihood estimate for \(\boldsymbol{\beta}\) by maximizing \(l(\boldsymbol{\beta})\). While it is possible to this with a numerical method like Newton’s method, there is a more clever way.
Maximizing the log-likelihood
To maximize the likelihood we will use a method first given by Zermelo in 1929. Given any starting \(\boldsymbol{\beta}^{(0)}\), we update it in the following way
\(\beta_k^{(t+1)}=\ln\left(\sum^n_{j=1}w_{kj}\right)-\ln\left(\sum_{j\ne k}\frac{w_{kj}+w_{jk}}{e^{\beta_k^{(t)}}+e^{\beta_j^{(t)}}}\right).\)
This will ensure that the sequence \({\boldsymbol{\beta}^{(t)}}\) will converge to the maximum likelihood estimator. To ensure uniqueness all that is required to keep a \(\beta_k\) fixed.
Confidence intervals
To determine the confidence intervals for the parameters we will make use of the likelihood ratio test. If \(\Theta_0\) is a restriction on the full parameter space \(\Theta\), then likelihood test statistic is given by
\(\lambda_{\text{LR}}=-2\ln\left(\frac{\text{sup}_{\boldsymbol{\beta}\in\Theta_0}l(\boldsymbol{\beta})}{\text{sup}_{\boldsymbol{\beta}\in\Theta}l(\boldsymbol{\beta})}\right).\)
Asymptotically we have that \(\lambda_{\text{LR}}\xrightarrow{d}\chi^2\). Here the \(\chi ^{2}\) distribution has degrees of freedom equal to the difference in dimensionality of \(\Theta\) and \(\Theta_0\).
Subsequently, \(A_k\) is a 95 percent confidence interval for \(\beta_k\) if,
\[x\in A_k \Leftrightarrow \lambda_{LR}\le\chi^2_{1,0.95} \text{ using } \Theta_0=\{\boldsymbol{\beta}\in\mathbb{R}^n|\beta_k=x\}.\]
Note that since \(l(\boldsymbol{\beta})\) is concave \(A_k\) will be convex and therefore connected. As \(A_k\) is connected it is defined by its endpoints. We can approximate these by noting the following:
\[\text{sup}_{\boldsymbol{\beta}\in\Theta_0}l(\boldsymbol{\beta})\approx l(\boldsymbol{\beta}^*+x\cdot e_k)\text{ with }\boldsymbol{\beta}^*=\text{argsup}_{\boldsymbol{\beta}\in\Theta}l(\boldsymbol{\beta}).\]
Which will give use that
\(\lambda_{\text{LR}}\approx 2l(\boldsymbol{\beta}^*) - 2l(\boldsymbol{\beta}^*+x\cdot e_k)=-2x\sum^n_{j\ne k}w_{kj}+2\sum^n_{j\ne k}\left(w_{kj}+w_{jk}\right)\left(\ln\left(e^{\beta_k+x}+e^{\beta_j}\right)-\ln\left(e^{\beta_k}+e^{\beta_j}\right)\right).\)
Then the endpoints of \(A_k\) can by computed by finding the two roots of \(\lambda_{\text{LR}}-\chi^2_{1,0.95}=0\).
Computation
I have written a small program to compute the maximum likelihood estimate and their 95 percent confidence intervals. To solve \(\lambda_{\text{LR}}-\chi^2_{1,0.95}=0\) Newton’s method was used. The program will read an excel csv file which is structured like so
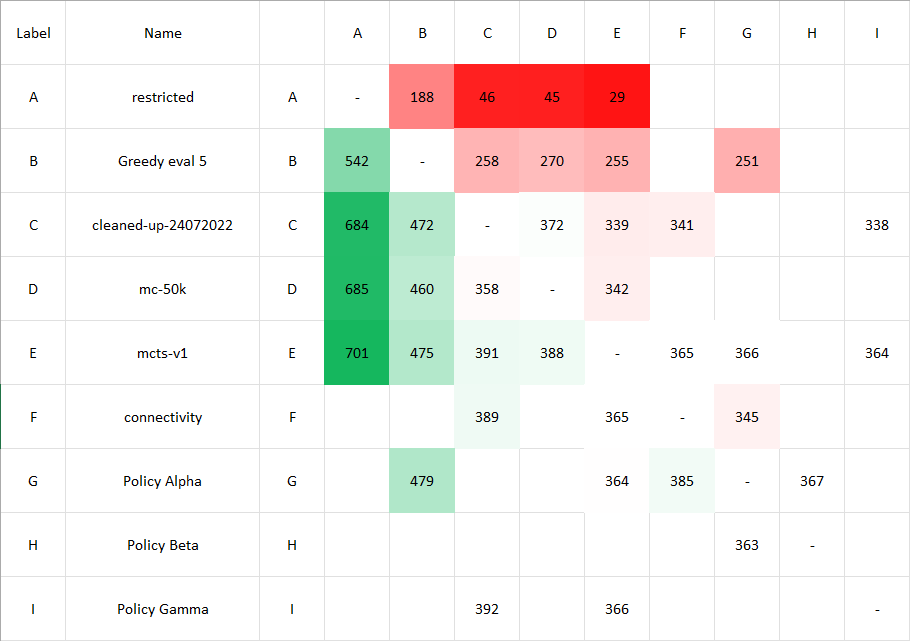
The code can be found here.